The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each spring in a lake.
A dynamical system has a state determined by a collection of real numbers, or more generally by a set of points in an appropriate state space. Small changes in the state of the system correspond to small changes in the numbers. The numbers are also the coordinates of a geometrical space—a manifold. The evolution rule of the dynamical system is a fixed rule that describes what future states follow from the current state. The rule is deterministic: for a given time interval only one future state follows from the current state.
Overview
Main article: Dynamical system (definition) Basic definitions
Basic definitions
The evolution function Φ are often ordinary differential equations: in this case the phase space M is a finite dimensional manifold. Many of the concepts in dynamical systems can be extended to infinite-dimensional manifolds—those that are locally Banach spaces—in which case the differential equations are partial differential equations. In the late 20th century the dynamical system perspective to partial differential equations started gaining popularity.
Examples
Logistic map
Double pendulum
Arnold's cat map
Horseshoe map
Baker's map is an example of a chaotic piecewise linear map
Billiards and outer billiards
Hénon map
Lorenz system
Circle map
Rössler map
List of chaotic maps
Swinging Atwood's machine
Quadratic map simulation system
Bouncing ball simulation system Further examples
 Basic definitions
Basic definitionsThe evolution function Φ are often ordinary differential equations: in this case the phase space M is a finite dimensional manifold. Many of the concepts in dynamical systems can be extended to infinite-dimensional manifolds—those that are locally Banach spaces—in which case the differential equations are partial differential equations. In the late 20th century the dynamical system perspective to partial differential equations started gaining popularity.
Examples
Logistic map
Double pendulum
Arnold's cat map
Horseshoe map
Baker's map is an example of a chaotic piecewise linear map
Billiards and outer billiards
Hénon map
Lorenz system
Circle map
Rössler map
List of chaotic maps
Swinging Atwood's machine
Quadratic map simulation system
Bouncing ball simulation system Further examples
Main article: Linear dynamical system Linear dynamical systems
For a flow, the vector field Φ(x) is a linear function of the position in the phase space, that is,
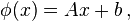
with A a matrix, b a vector of numbers and x the position vector. The solution to this system can be found by using the superposition principle (linearity). The case b ≠ 0 with A = 0 is just a straight line in the direction of b:

When b is zero and A ≠ 0 the origin is an equilibrium (or singular) point of the flow, that is, if x0 = 0, then the orbit remains there. For other initial conditions, the equation of motion is given by the exponential of a matrix: for an initial point x0,

When b = 0, the eigenvalues of A determine the structure of the phase space. From the eigenvalues and the eigenvectors of A it is possible to determine if an initial point will converge or diverge to the equilibrium point at the origin.
The distance between two different initial conditions in the case A ≠ 0 will change exponentially in most cases, either converging exponentially fast towards a point, or diverging exponentially fast. Linear systems display sensitive dependence on initial conditions in the case of divergence. For nonlinear systems this is one of the (necessary but not sufficient) conditions for chaotic behavior.
Maps
The qualitative properties of dynamical systems do not change under a smooth change of coordinates (this is sometimes taken as a definition of qualitative): a singular point of the vector field (a point where v(x) = 0) will remain a singular point under smooth transformations; a periodic orbit is a loop in phase space and smooth deformations of the phase space cannot alter it being a loop. It is in the neighborhood of singular points and periodic orbits that the structure of a phase space of a dynamical system can be well understood. In the qualitative study of dynamical systems, the approach is to show that there is a change of coordinates (usually unspecified, but computable) that makes the dynamical system as simple as possible.
Local dynamics
A flow in most small patches of the phase space can be made very simple. If y is a point where the vector field v(y) ≠ 0, then there is a change of coordinates for a region around y where the vector field becomes a series of parallel vectors of the same magnitude. This is known as the rectification theorem.
The rectification theorem says that away from singular points the dynamics of a point in a small patch is a straight line. The patch can sometimes be enlarged by stitching several patches together, and when this works out in the whole phase space M the dynamical system is integrable. In most cases the patch cannot be extended to the entire phase space. There may be singular points in the vector field (where v(x) = 0); or the patches may become smaller and smaller as some point is approached. The more subtle reason is a global constraint, where the trajectory starts out in a patch, and after visiting a series of other patches comes back to the original one. If the next time the orbit loops around phase space in a different way, then it is impossible to rectify the vector field in the whole series of patches.
Rectification
In general, in the neighborhood of a periodic orbit the rectification theorem cannot be used. Poincaré developed an approach that transforms the analysis near a periodic orbit to the analysis of a map. Pick a point x0 in the orbit γ and consider the points in phase space in that neighborhood that are perpendicular to v(x0). These points are a Poincaré section S(γ, x0), of the orbit. The flow now defines a map, the Poincaré map F : S → S, for points starting in S and returning to S. Not all these points will take the same amount of time to come back, but the times will be close to the time it takes x0.
The intersection of the periodic orbit with the Poincaré section is a fixed point of the Poincaré map F. By a translation, the point can be assumed to be at x = 0. The Taylor series of the map is F(x) = J · x + O(x²), so a change of coordinates h can only be expected to simplify F to its linear part

This is known as the conjugation equation. Finding conditions for this equation to hold has been one of the major tasks of research in dynamical systems. Poincaré first approached it assuming all functions to be analytic and in the process discovered the non-resonant condition. If λ1,…,λν are the eigenvalues of J they will be resonant if one eigenvalue is an integer linear combination of two or more of the others. As terms of the form λi – ∑ (multiples of other eigenvalues) occurs in the denominator of the terms for the function h, the non-resonant condition is also known as the small divisor problem.
Near periodic orbits
The results on the existence of a solution to the conjugation equation depend on the eigenvalues of J and the degree of smoothness required from h. As J does not need to have any special symmetries, its eigenvalues will typically be complex numbers. When the eigenvalues of J are not in the unit circle, the dynamics near the fixed point x0 of F is called hyperbolic and when the eigenvalues are on the unit circle and complex, the dynamics is called elliptic.
In the hyperbolic case the Hartman-Grobman theorem gives the conditions for the existence of a continuous function that maps the neighborhood of the fixed point of the map to the linear map J · x. The hyperbolic case is also structurally stable. Small changes in the vector field will only produce small changes in the Poincaré map and these small changes will reflect in small changes in the position of the eigenvalues of J in the complex plane, implying that the map is still hyperbolic.
The Kolmogorov-Arnold-Moser (KAM) theorem gives the behavior near an elliptic point.
Conjugation results
For a flow, the vector field Φ(x) is a linear function of the position in the phase space, that is,
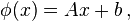
with A a matrix, b a vector of numbers and x the position vector. The solution to this system can be found by using the superposition principle (linearity). The case b ≠ 0 with A = 0 is just a straight line in the direction of b:

When b is zero and A ≠ 0 the origin is an equilibrium (or singular) point of the flow, that is, if x0 = 0, then the orbit remains there. For other initial conditions, the equation of motion is given by the exponential of a matrix: for an initial point x0,

When b = 0, the eigenvalues of A determine the structure of the phase space. From the eigenvalues and the eigenvectors of A it is possible to determine if an initial point will converge or diverge to the equilibrium point at the origin.
The distance between two different initial conditions in the case A ≠ 0 will change exponentially in most cases, either converging exponentially fast towards a point, or diverging exponentially fast. Linear systems display sensitive dependence on initial conditions in the case of divergence. For nonlinear systems this is one of the (necessary but not sufficient) conditions for chaotic behavior.
Maps
The qualitative properties of dynamical systems do not change under a smooth change of coordinates (this is sometimes taken as a definition of qualitative): a singular point of the vector field (a point where v(x) = 0) will remain a singular point under smooth transformations; a periodic orbit is a loop in phase space and smooth deformations of the phase space cannot alter it being a loop. It is in the neighborhood of singular points and periodic orbits that the structure of a phase space of a dynamical system can be well understood. In the qualitative study of dynamical systems, the approach is to show that there is a change of coordinates (usually unspecified, but computable) that makes the dynamical system as simple as possible.
Local dynamics
A flow in most small patches of the phase space can be made very simple. If y is a point where the vector field v(y) ≠ 0, then there is a change of coordinates for a region around y where the vector field becomes a series of parallel vectors of the same magnitude. This is known as the rectification theorem.
The rectification theorem says that away from singular points the dynamics of a point in a small patch is a straight line. The patch can sometimes be enlarged by stitching several patches together, and when this works out in the whole phase space M the dynamical system is integrable. In most cases the patch cannot be extended to the entire phase space. There may be singular points in the vector field (where v(x) = 0); or the patches may become smaller and smaller as some point is approached. The more subtle reason is a global constraint, where the trajectory starts out in a patch, and after visiting a series of other patches comes back to the original one. If the next time the orbit loops around phase space in a different way, then it is impossible to rectify the vector field in the whole series of patches.
Rectification
In general, in the neighborhood of a periodic orbit the rectification theorem cannot be used. Poincaré developed an approach that transforms the analysis near a periodic orbit to the analysis of a map. Pick a point x0 in the orbit γ and consider the points in phase space in that neighborhood that are perpendicular to v(x0). These points are a Poincaré section S(γ, x0), of the orbit. The flow now defines a map, the Poincaré map F : S → S, for points starting in S and returning to S. Not all these points will take the same amount of time to come back, but the times will be close to the time it takes x0.
The intersection of the periodic orbit with the Poincaré section is a fixed point of the Poincaré map F. By a translation, the point can be assumed to be at x = 0. The Taylor series of the map is F(x) = J · x + O(x²), so a change of coordinates h can only be expected to simplify F to its linear part

This is known as the conjugation equation. Finding conditions for this equation to hold has been one of the major tasks of research in dynamical systems. Poincaré first approached it assuming all functions to be analytic and in the process discovered the non-resonant condition. If λ1,…,λν are the eigenvalues of J they will be resonant if one eigenvalue is an integer linear combination of two or more of the others. As terms of the form λi – ∑ (multiples of other eigenvalues) occurs in the denominator of the terms for the function h, the non-resonant condition is also known as the small divisor problem.
Near periodic orbits
The results on the existence of a solution to the conjugation equation depend on the eigenvalues of J and the degree of smoothness required from h. As J does not need to have any special symmetries, its eigenvalues will typically be complex numbers. When the eigenvalues of J are not in the unit circle, the dynamics near the fixed point x0 of F is called hyperbolic and when the eigenvalues are on the unit circle and complex, the dynamics is called elliptic.
In the hyperbolic case the Hartman-Grobman theorem gives the conditions for the existence of a continuous function that maps the neighborhood of the fixed point of the map to the linear map J · x. The hyperbolic case is also structurally stable. Small changes in the vector field will only produce small changes in the Poincaré map and these small changes will reflect in small changes in the position of the eigenvalues of J in the complex plane, implying that the map is still hyperbolic.
The Kolmogorov-Arnold-Moser (KAM) theorem gives the behavior near an elliptic point.
Conjugation results
Main article: Bifurcation theory Bifurcation theory
Main article: ergodic theory Ergodic systems
Main article: chaos theory Chaos theory
Dynamic system theory has recently emerged in the field of cognitive development. It is the belief that cognitive development is best represented by physical theories rather than theories based on syntax and AI. In it, the learner's mind reaches a state of disequilibrium where old patterns have broken down. This is the phase transition of cognitive development. Self organization (sponteanous creation of coherent forms) sets in as activity (a.k.a energy) levels link to each other. Newly formed macroscopic and microscopic structures support each other, speeding up the process. These links form the structure of a new state of order in the mind through a process called scalloping (the repeated building up and collapsing of complex performance.) This new, novel state is progressive, discrete, idiosyncratic and unpredictable.
See also
Works providing a broad coverage:
Introductory texts with a unique perspective:
Textbooks
Popularizations:
Ralph Abraham and Jerrold E. Marsden (1978). Foundations of mechanics. Benjamin-Cummings. ISBN 0-8053-0102-X. (available as a reprint: ISBN 0-201-40840-6)
Encyclopaedia of Mathematical Sciences (ISSN 0938-0396) has a sub-series on dynamical systems with reviews of current research.
Anatole Katok and Boris Hasselblatt (1996). Introduction to the modern theory of dynamical systems. Cambridge. ISBN 0-521-57557-5.
Christian Bonatti, Lorenzo J. Díaz, Marcelo Viana (2005). Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective. Springer. ISBN 3-540-22066-6.
Diederich Hinrichsen and Anthony J. Pritchard (2005). Mathematical Systems Theory I - Modelling, State Space Analysis, Stability and Robustness. Springer Verlag. ISBN 0-978-3-540-44125-0.
V. I. Arnold (1982). Mathematical methods of classical mechanics. Springer-Verlag. ISBN 0-387-96890-3.
Jacob Palis and Wellington de Melo (1982). Geometric theory of dynamical systems: an introduction. Springer-Verlag. ISBN 0-387-90668-1.
David Ruelle (1989). Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. ISBN 0-12-601710-7.
Tim Bedford, Michael Keane and Caroline Series, eds. (1991). Ergodic theory, symbolic dynamics and hyperbolic spaces. Oxford University Press. ISBN 0-19-853390-X.
Ralph H. Abraham and Christopher D. Shaw (1992). Dynamics—the geometry of behavior, 2nd edition. Addison-Wesley. ISBN 0-201-56716-4.
Steven H. Strogatz (1994). Nonlinear dynamics and chaos: with applications to physics, biology chemistry and engineering. Addison Wesley. ISBN 0-201-54344-3.
Kathleen T. Alligood, Tim D. Sauer and James A. Yorke (2000). Chaos. An introduction to dynamical systems. Springer Verlag. ISBN 0-387-94677-2.
Morris W. Hirsch, Stephen Smale and Robert Devaney (2003). Differential Equations, dynamical systems, and an introduction to chaos. Academic Press. ISBN 0-12-349703-5.
Florin Diacu and Philip Holmes (1996). Celestial Encounters. Princeton. ISBN 0-691-02743-9.
James Gleick (1988). Chaos: Making a New Science. Penguin. ISBN 0-14-009250-1.
Ivar Ekeland (1990). Mathematics and the Unexpected (Paperback). University Of Chicago Press. ISBN 0-226-19990-8.
Dynamic system theory has recently emerged in the field of cognitive development. It is the belief that cognitive development is best represented by physical theories rather than theories based on syntax and AI. In it, the learner's mind reaches a state of disequilibrium where old patterns have broken down. This is the phase transition of cognitive development. Self organization (sponteanous creation of coherent forms) sets in as activity (a.k.a energy) levels link to each other. Newly formed macroscopic and microscopic structures support each other, speeding up the process. These links form the structure of a new state of order in the mind through a process called scalloping (the repeated building up and collapsing of complex performance.) This new, novel state is progressive, discrete, idiosyncratic and unpredictable.
See also
Works providing a broad coverage:
Introductory texts with a unique perspective:
Textbooks
Popularizations:
Ralph Abraham and Jerrold E. Marsden (1978). Foundations of mechanics. Benjamin-Cummings. ISBN 0-8053-0102-X. (available as a reprint: ISBN 0-201-40840-6)
Encyclopaedia of Mathematical Sciences (ISSN 0938-0396) has a sub-series on dynamical systems with reviews of current research.
Anatole Katok and Boris Hasselblatt (1996). Introduction to the modern theory of dynamical systems. Cambridge. ISBN 0-521-57557-5.
Christian Bonatti, Lorenzo J. Díaz, Marcelo Viana (2005). Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective. Springer. ISBN 3-540-22066-6.
Diederich Hinrichsen and Anthony J. Pritchard (2005). Mathematical Systems Theory I - Modelling, State Space Analysis, Stability and Robustness. Springer Verlag. ISBN 0-978-3-540-44125-0.
V. I. Arnold (1982). Mathematical methods of classical mechanics. Springer-Verlag. ISBN 0-387-96890-3.
Jacob Palis and Wellington de Melo (1982). Geometric theory of dynamical systems: an introduction. Springer-Verlag. ISBN 0-387-90668-1.
David Ruelle (1989). Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. ISBN 0-12-601710-7.
Tim Bedford, Michael Keane and Caroline Series, eds. (1991). Ergodic theory, symbolic dynamics and hyperbolic spaces. Oxford University Press. ISBN 0-19-853390-X.
Ralph H. Abraham and Christopher D. Shaw (1992). Dynamics—the geometry of behavior, 2nd edition. Addison-Wesley. ISBN 0-201-56716-4.
Steven H. Strogatz (1994). Nonlinear dynamics and chaos: with applications to physics, biology chemistry and engineering. Addison Wesley. ISBN 0-201-54344-3.
Kathleen T. Alligood, Tim D. Sauer and James A. Yorke (2000). Chaos. An introduction to dynamical systems. Springer Verlag. ISBN 0-387-94677-2.
Morris W. Hirsch, Stephen Smale and Robert Devaney (2003). Differential Equations, dynamical systems, and an introduction to chaos. Academic Press. ISBN 0-12-349703-5.
Florin Diacu and Philip Holmes (1996). Celestial Encounters. Princeton. ISBN 0-691-02743-9.
James Gleick (1988). Chaos: Making a New Science. Penguin. ISBN 0-14-009250-1.
Ivar Ekeland (1990). Mathematics and the Unexpected (Paperback). University Of Chicago Press. ISBN 0-226-19990-8.
No comments:
Post a Comment